Содержание
Произвольное следование: выкладка линейной дракон-модели
Для начала рассмотрим визуализацию линейной последовательности операторов на техноязыке.

Следование в техноязыке – визуальное определение
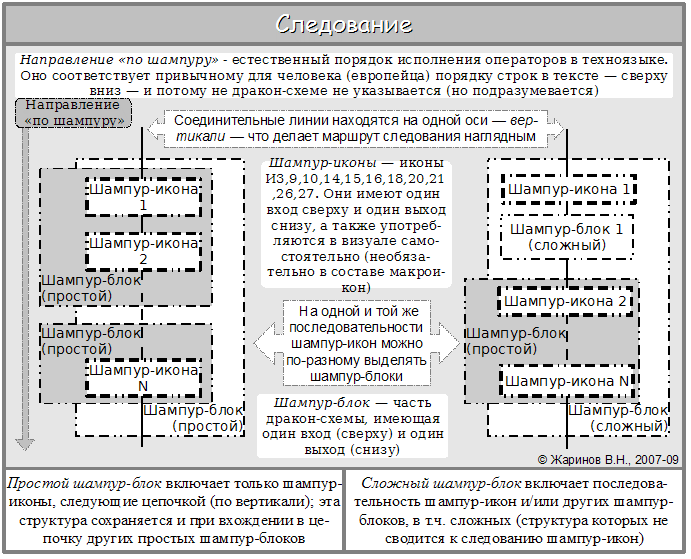
Последовательность неэлементарна потому, что в техноязыке она определяется как цепочка шампур-блоков, внутри которых содержатся не только шампур-иконы, но и другие шампур-блоки. Иначе, последовательность как цепочка икон Действие или других шампур-икон (соответствует следованию в блок-схемах) на техноязыке – только один из видов содержания шампур-блока (в частном случае она состоит из одной шампур-иконы); такой шампур-блок назовем простым. Другой вид (более общий) – структура, в которой присутствуют любые типы вершин, включая элементы ветвлений и циклов – развилки, переключатели, петли (в блок-схемах – предикатные и соединительные вершины с линиями обратной и/или прямой связи), причем через каждую вершину проходит хотя бы один путь от входа к выходу; назовем её сложным шампур-блоком.
Чем отличается простой шампур-блок от сложного? В первом мы можем выделять мелкие шампур-блоки вполне произвольно (с одним ограничением — чтобы границы их соприкасались, но не накладывались — можно только выделить более мелкий блок целиком внутри более крупного). Во втором этого недостаточно — мелкий блок не д.б. нешампур-блоком — т.е. разбиение ограничено структурой разбиваемого блока.
Далее мы будем иметь дело в основном со сложными шампур-блоками. Кроме того, в дракон-схемах формы силуэта допустимы блоки иного рода, называемые адресными – в которых вход по-прежнему один, но выходов два и более (подробно рассмотрены далее).
Итак, представление одной и той же деятельности в виде последовательности (цепочки действий) в общем случае неоднозначно; поэтому шампур-блок и принят за базовую конструкцию техноязыка в отличие от серии (композиции) в блок-схемах.
В качестве примера неоднозначности рассмотрим задачу вычисления некоторых величин на основании предварительно введенных исходных данных с последующей выдачей результатов.
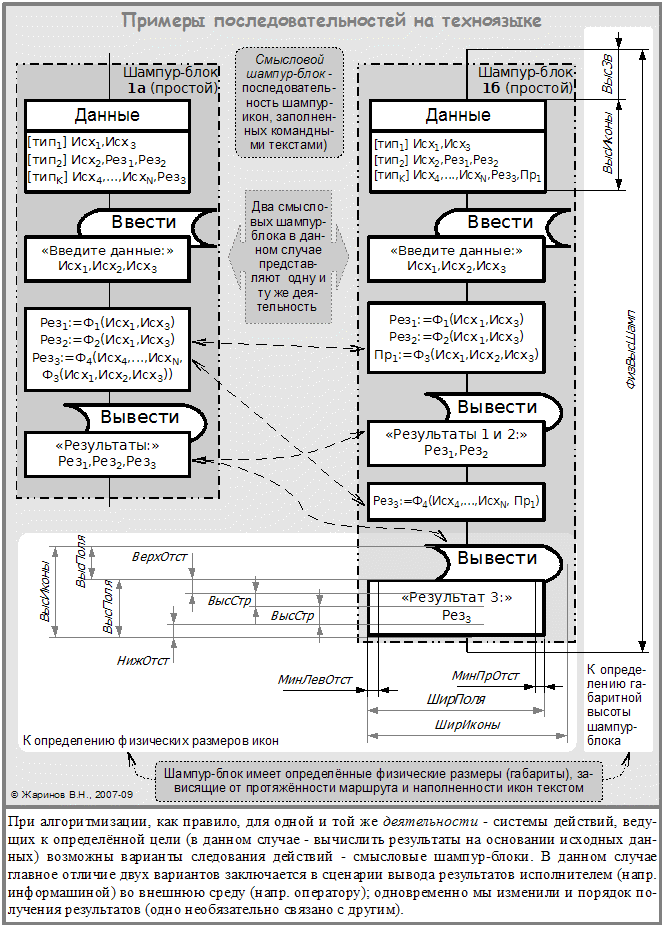
Следование в техноязыке – примеры конструкций
Когда содержание икон неважно для работы над дракон-схемой, текст каждой иконы можно заменить литеральным обозначением (буквой некоторой азбуки), причем одинаковым текстам соответствуют разные буквы, а разным текстам – разные (то же делается, когда точные тексты икон ещё неясны). Такой вариант визуала называется литеральной записью (тогда как запись с содержательным текстом – смысловой).
Если разных текстов больше, чем букв азбуки, можно использовать аббревиатуры; для отражения к.-л. подразделения икон также можно усложнить правила обозначения (скажем, вводить цифровые или иные индексы, в т.ч. иерархические).
В качестве примера в литеральной записи даны предыдущие шампур-блоки.
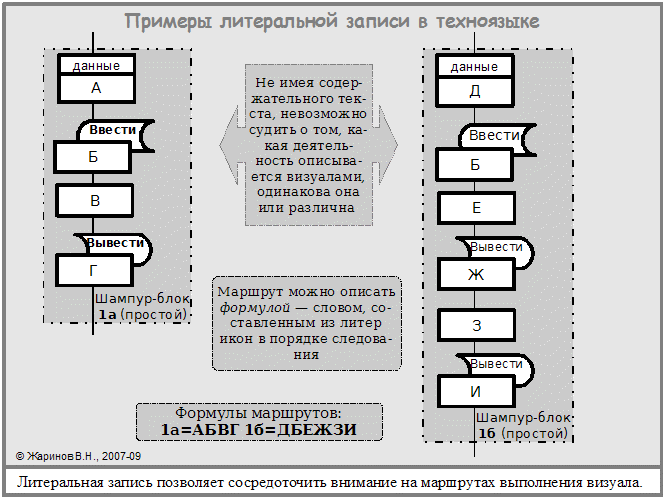
Литеральная запись текста визуала
Литеральная запись экономит площадь за счет сокращения габаритов икон. Она позволяет формально описать структуры управления (маршруты выполнения) алгоритмов.
Маршрут визуала (линейного) – путь по дракон-схеме от начала до конца, проходящий через иконы и соединительные линии.
Формула маршрута – последовательность литер, обозначающих иконы.
Также определим некоторые отношения между двумя произвольными алгоритмами.
Равносильные алгоритмы – такие, у которых все маршруты попарно одинаковы (имеют совпадающие формулы).
Эквивалентные алгоритмы – дающие одинаковые результаты при одних и тех же исходных данных.
Равносильные алгоритмы всегда эквивалентны. Обратное утверждение неверно, в чем легко убедиться из вышеприведенных примеров (которые для этого утверждения служат контрпримерами, т.е. примерами-опровержениями).
Пунктирные стрелки показывают эквивалентные преобразования линейного алгоритма – перераспределения действий по маршруту. Равносильное преобразование может состоять, напр. в замене имен некоторых величин, функций в тексте всех икон; формула алгоритма от этого не меняется (поскольку тексты, которые были одинаковы до такой замены, остаются одинаковы и после нее, аналогично и различные тексты остаются различными).
По литеральной записи неравносильных алгоритмов невозможно установить, эквивалентны они или нет.
Идя далее в абстрагировании записи, можно совсем исключить из дракон-схемы текст; получается чертеж, называемый абстрактной дракон-схемой («слепышом») и содержащий только операторы маршрутного подъязыка ДРАКОНа. Абстрактная запись удобна для представления и сравнительного анализа структур управления алгоритмов независимо от их содержания, а также формализованного описания самого техноязыка.
Сопоставим теперь шампур-блок с линейной конструкцией традиционных блок-схем (серией функциональных вершин); обе структуры дадим как слепыши (см. «очную ставку»).
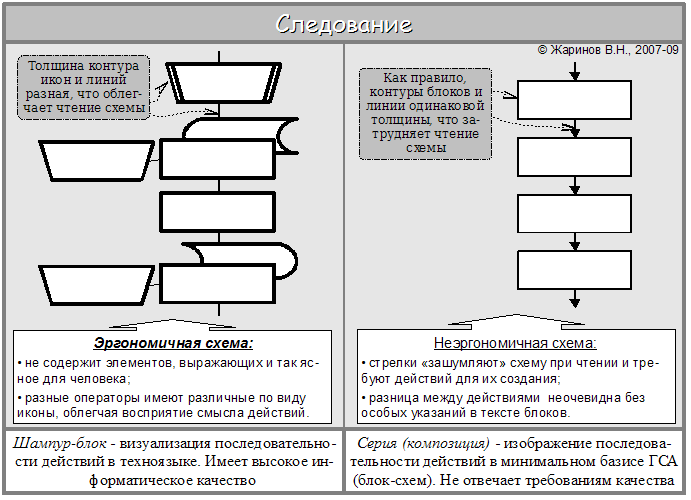
Следование – «очная ставка» на техноязыке и языке блок-схем
Маршруты отражают структуру управления алгоритма. Кроме того, формулы маршрутов в текстовой форме описывают топологию дракон-схемы (это термин, означающий математическое описание пространственного строения любого объекта).
Топология – важная и сложная отрасль математики; но нам нужны лишь её отдельные элементы, которые часто можно визуализировать для лучшего понимания.
Применительно к линейным визуалам можно говорить о такой топологической характеристике, как длина маршрута. Очевидно, у эквивалентных алгоритмов эта длина м.б. неодинакова, хотя результат их исполнения один и тот же по определению. Что же меняется? Число и порядок звеньев вертикали, а значит, и естественных переходов (каждому соответствует звено), и точек вставки (помещенных посредине звена), и различимых состояний исполнителя.
Ограничения на топологию дракон-схем описаны в стандарте техноязыка как часть текста отдельных тезисов (см. /1, Гл.15/). Главное ограничение для линейной структуры – не допускается разрыв шампура на части между разными диосценами (напр. листами, на которых чертится дракон-схема сочиняемого визуала). Для этого физическая высота схемы (шампура вместе с границами) не должна превышать высоты рабочего поля диосцены.
Обсудим, как удовлетворить этому. В основном высота схемы зависит от шампура:
ФизВысШамп = сумма(ДлЗвена) + сумма(ВысЭлИконы), где:
ДлЗвена – длина звена вертикали; ВысЭлИконы – высота элемента иконы, причем:
ВысЭлИконы = ВерхОтст + (КолСтр * ВысСтр) + НижОтст, здесь:
ВерхОтст – отступ первой строки текста от верхнего контура иконы (её элемента).
НижОтст – отступ последней строки текста от нижнего контура иконы (её элемента).
КолСтр – число строк текста в очередном по высоте (единственном) элементе иконы;
ВысСтр – полная высота строки текста (для данного абзаца) в очередном элементе иконы, причём:
ВысСтр = Кегль * ИнтСтр, здесь:
Кегль – (типографское) принятая высота шрифта текста; измеряется по ядру строчных букв;
ИнтСтр – межстрочный интервал для абзаца текста в очередном элементе иконы.
Все эти величины вместе можно назвать вертикальными параметрами компоновки; для ДлЗвена, Кегль, ИнтСтр, *Отст минимальные значения задаются из эргономических соображений (читабельности текста).
Из алфавита видно, что отдельные иконы имеют несколько элементов-полей, в т.ч. перекрывающихся; для них ширина задаётся по одному из полей, принятому за базовое, а высотой считается вертикальный размер видимой части элемента.
Дракон-схема предназначена человеку т.е. имеет символическую форму, а основным её представлением является бумажный (печатный) документ. При типографском качестве отображения (печати) или близком к нему (напр. лазерной принтописи) кегль текста выбирают в пределах 10...12 пунктов (зависит и от выбранной гарнитуры шрифта); допустим межстрочный интервал от 10...20% кегля, а отступ первой строки – порядка 0,1 см.
Кроме кегля, на итоговый пиксельный размер букв текста влияет и гарнитура шрифта. В разных полях икон она м.б. различна для удобства восприятия; мы выбрали конкретные гарнитуры. Тогда величина КолСтр определяется горизонтальными параметрами компоновки: шириной иконы (поля) и отступами текста от контура слева и справа:
ШирСтр = ШирПоля – (МинЛевОтст + МинПрОтст)
Обычно для одной дракон-схемы выбирают эти параметры постоянными.
Напомним, что при вводе текста в фигуры, как и на страницу, приложение редактирования производит т.н. выключку – автоматическое размещение текста в строках заданной ширины.
Алгоритм выключки в фигурах для типичного офисного пакета следующий. По завершении ввода в абзац (как «жёсткий», заданный нажатием <Enter>, так и «мягкий» – с сохранением стиля, заданный нажатием <Shift>+<Enter>) текст абзаца построчно, начиная с места ввода, перераспределяется так, чтобы суммарная ширина букв в строке (включая знаки пробела) была меньше ШирСтр; при этом, если включена расстановка переносов, то последнее слово переносится, а если для абзаца задано выравнивание по ширине, то каждый пробел также «разгоняется» настолько, чтобы дополнить нехватку ширины до ШирСтр; в итоге КолСтр может измениться, и габаритная высота текста определяется заново по вышеприведённому выражению для ВысЭлИконы. Далее, если в фигуре включено свойство Подогнать под текст , то высота фигуры меняется так, чтобы удовлетворить новому ВысЭлИконы; иначе выключенный текст остаётся в новой габаритной высоте, «недотягивая» до нижнего/верхнего краёв контура либо «выпирая» за них, а высоту контура нужно изменять вручную.
Итак, меняя кегль, межстрочный интервал и отступы для некоторого элемента иконы, мы можем в определённой степени влиять на число строк текста в этом элементе, а значит, и на его высоту. Последняя строка чаще всего неполная, т.н. «хвост».
От заданных параметров и зависит минимальный физический размер конкретного шампура. В целях рациональной компоновки можно управлять размером, меняя некоторые параметры.
Аналогично можно управлять высотой элементов границ шампура (икон и «гребёнок»).
Исходя из эргономичности, в реальной дракон-схеме промежутки между соседними иконами д. б. различимы, а отступы текста от контура иконы (её части) – заметны на глаз.
Если такая подгонка не даёт результата (схема не умещается на выбранном формате целиком), то в частном случае можно пойти на отступления от правил компоновки; однако в общем случае это невозможно и возникает проблема. Для её решения можно применить подстановку, но уже не как формальную операцию оформления инварианта, а как неформальный эргономический приём. В этом случае границы фрагмента, выносимого во вставку, определяются тем, насколько нужно сократить высоту шампура.
Традиционно (в блок-схемах) допускается разрывать линии между листами, вставляя вершины-соединители. Такую схему читать неудобно, да и сочинять сложно; поэтому и запрещены разрывы в техноязыке. Однако это справедливо для диосцены (двумерного пространства); а как дело обстоит в одномерном (логически) пространстве? Рассмотрим это далее.
Ранее мы рассмотрели содержание подстановки и иконы Вставка. Безусловный переход м.б. использован внутри шампура и более общим образом; покажем это.
Мы уже изобрели новые визуальные операторы для обозначения шампур-блоков и нелинейных фрагментов дракон-схем, использованные при анализе в п/р 2.1. Теперь изобретём обозначения для безусловного перехода с возвратом; они нам понадобятся для начала. Логично доработать БП-иконы техноязыка, введя по аналогии со вставкой вторые вертикальные линии контура. Текст иконы Адрес вставки (назовём её так) аналогичен по формату тексту иконы Вставка; у иконы Имя вставки текст составляется из текстов икон Заголовок и Формальные параметры по тому же принципу. Тем самым мы исключаем икону И11 из нашей записи.
Перерисуем дракон-модель из п/п 2.3.1.3 в такой нотации; результат см. схему далее.
Очевидно, что можно считать полученные структуры частями одного шампура. Теперь введём линейный порядок частей шампура, т.е. выложим нашу модель в цепочку. Оказывается, это можно сделать не единственным образом; имеются разные варианты следования частей (т.н. перестановки). Число вариантов определяется комбинаторной формулой перестановок и для нашего случая (3 части) равно 6, мы покажем три (на рисунке далее).
Теперь представим себе, что мы проделываем то же самое, разделяя шампур на части уже обычными БП; в отличие от БП с возвратом, здесь не требуется сохранять/восстанавливать состояния, поскольку исполняется всё тот же алгоритм.
Эти переходы по содержанию эквивалентны совершаемым в петле силуэта разрешённым БП, но имеют иное назначение; поэтому изобретём обозначения и для них. Воспользуемся для иконы-метки графикой иконы Вариант, а для иконы-команды соответственно отразим эту фигуру по горизонтальной оси. Такое решение удобно будет при дальнейшем употреблении этого типа перехода.
С т. зр. классического техноязыка это вроде бы недопустимая схема: имеем линии, которые обрываются, не достигая иконы Конец (Паронджанов называет их «хвосты»). Однако смысл безусловного перехода ставит всё на свои места; части можно рассматривать как аналоги визуалов-вставок, только без особенностей БП с возвратом. Правда, это уже не классический ДРАКОН; по сути, мы модифицировали шампур-метод.
Для чего это нужно? Вспомним, что выкладка согласует топологию алгоритма с пространственными свойствами формального исполнителя — линейностью и конечностью его памяти. При этом некоторые участки этой памяти м.б. уже заняты служебными величинами исполнителя, содержанием других алгоритмов.
В общем случае заранее неизвестно, как расположатся эти участки и останется ли хотя бы одна свободная область, достаточная для размещения данного алгоритма. Значит, мы должны иметь возможность делить алгоритм на такие части, для каждой из которых найдётся место в памяти. Эту возможность нам и даёт введение в шампур обычных БП.
В такого рода структуре неважен и физический порядок следования частей в памяти друг относительно друга («как выложено»); адреса переходов логически свяжут части по порядку в шампуре («как сочинено»). Это даёт нам необходимую свободу выкладки при том, что объёмы частей м.б. различны; необязательно, что подходящие по объёму участки в памяти будут следовать в том же порядке, что и части выкладываемого шампура.
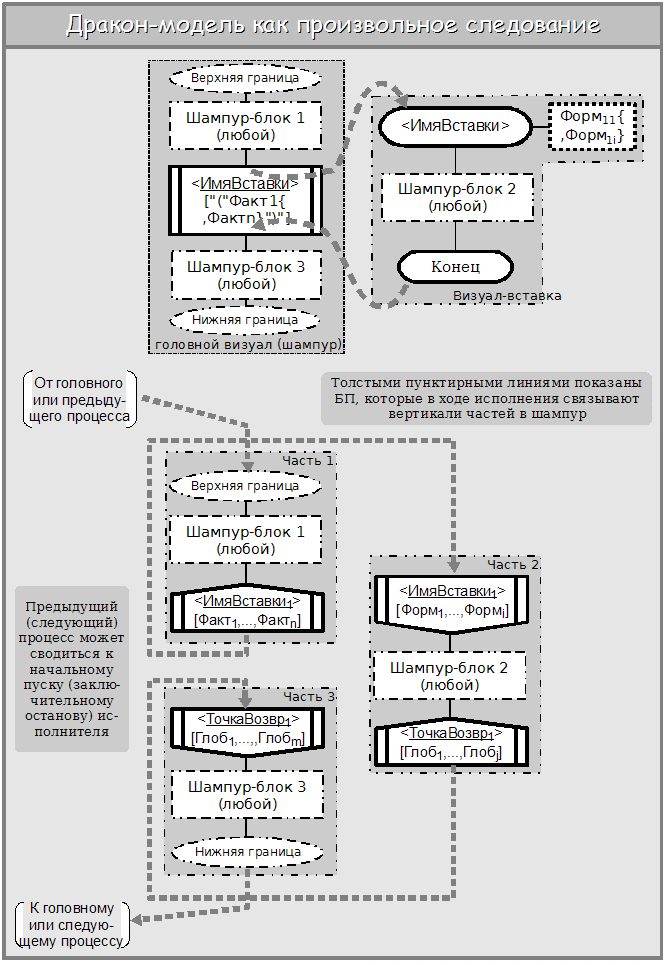
Безусловные переходы с возвратом в шампуре
Здесь мы следуем принципу упорядочения вертикалей (шампуров и переходов).
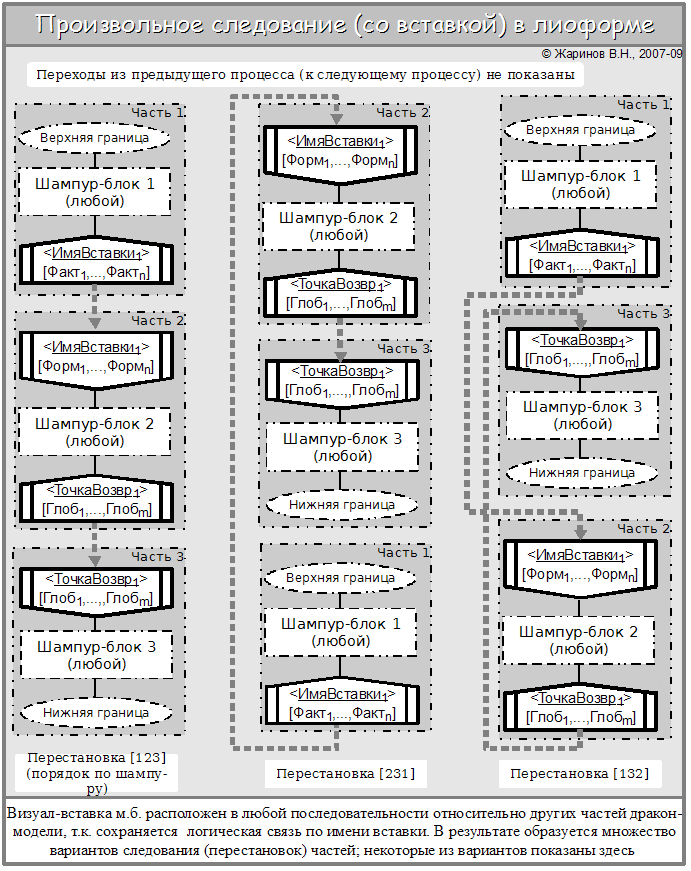
Примеры выкладки шампура, содержащего безусловные переходы с возвратом
Для выкладки каждая часть д.б. шампур-блоком (простым; над сложным вначале нужно выполнить некоторые операции, которых мы коснёмся далее).
Здесь даны три перестановки; ещё две приведены на следующей схеме. Очевидно, читателю не представит труда обнаружить и изобразить единственную оставшуюся для самообразования :)
По сути, речь идёт о компоновке визуала в лиоформе и предметном представлении (где фигура и текст каждой иконы заменены машинными кодами действий, отвечающих её смыслу).
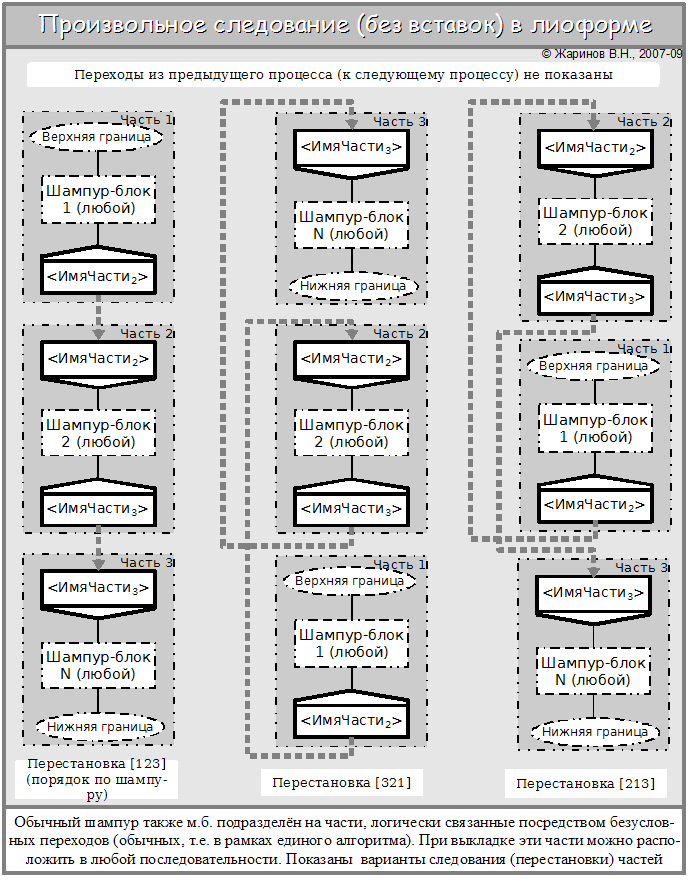
Примеры выкладки шампура, содержащего простые безусловные переходы
Это и есть случаи произвольного следования. Фактически мы объяснили принцип размещения машинного кода программы в основной памяти (ОП) информашины, не прибегая при этом к специфическим терминам и способам изложения, принятым в системном программировании; это лишний пример выразительной силы техноязыка (с введёнными выше знаками).
В начало страницы | Оглавление | Главная | Версия для печати
Copyright © Жаринов В.Н.